Question

The weights of Siamese cats are normally distributed with a mean of 6.4 pounds and a standard deviation of 0.8 pounds. If a breeder of Siamese cats has 128 in his care, how many can he expect to have weights between 5.2 and 7.6 pounds?

(1) 106 (3) 98

(2) 49 (4) 111

Answer 1

111 cats

Step-by-step explanation: Given that standard deviation = 0.8

Z score = ( raw score - mean ) ÷ standard deviation. Hence,

For 5.2: (5.2 - 6.4) / 0.8 = - 1.5 standard deviation is below the mean

For 7.6 : ( 7.6 - 6.4 )/ 0.8 = 1.5 standard deviation is above the mean

Thus: 2×( 19.1+ 15.0 +9.2 ) = 86.6%

and we now find:

0.866 × 128 = 110.848

~111 cats

Answer 2

(4) 111

Explanation:

Given that:

mean (μ) = 6.4 pounds

Standard deviation (σ) = 0.8 pounds

Number of Siamese cats (n) = 128

The z score (z) is given by the equation:

`z=(x-\mu)/(\sigma)`, Where x is the raw score.

For a raw score of 5.2 pounds:

`z=(x-\mu)/(\sigma)=(5.2-6.4)/(0.8)=-1.5`

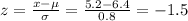
For a raw score of 7.6 pounds:

`z=(x-\mu)/(\sigma)=(7.6-6.4)/(0.8)=1.5`

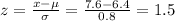
From the normal probability table:

P(5.2 < x < 7.6) = P(-1.5 < z < 1.5) = P(z < 1.5) - P(z < -1.5) = 0.9332 - 0.0668= 0.8664 = 86.64%

Therefore 86.64% of Siamese cats have weights between 5.2 and 7.6 pounds.

The number of Siamese cats that have weights between 5.2 and 7.6 pounds = 86.64% × n = 0.8664 × 128 ≈ 111