Question

To estimate the mean score μ of those who took the Medical College Admission Test on your campus, you will obtain the scores of an SRS of students. From published information you know that the scores are approximately Normal with standard deviation about 6.3 . You want your sample mean ¯ x to estimate μ with an error of no more than 1.3 point in either direction.

(a) What standard deviation must ¯ x have so that 99.7 % of all samples give an ¯ x within 1.3 point of μ ? Use the 68 – 95 – 99.7 rule. (Enter your answer rounded to four decimal places.)

(b) How large an SRS do you need in order to reduce the standard deviation of

¯

x

to the value you found? (Enter your answer rounded to the nearest whole number.)

Answer 1

a. 0.4333

b. 255

Explanation:

The maximum Error E is 1.3

approximately normal test scores,

Standard Deviation, SD is 6.5

a).

Level of confidence = 99.7%

critical value of z for a two tailed test and 0.3% level of significance is 3

since the sample mean is within 0.5 of the true population mean

hence, the standard dev of mean is given by

`Z_(\alpha)[(\sigma)/(√(n)) ]=E`

where E = 1.3

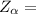`Z_(\alpha)=` 1.3

`(\sigma)/(√(n)) =(E)/(Z_(\alpha)) \\\\(\sigma)/(√(n)) =(1.3)/(3)`

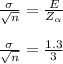
hence the Std of the mean is 0.4333 (to 4 d.p.)

b).

The sample size is computed as follows

making n the subject of formular of the above equation

`√(n) =(3\sigma)/(1.3)} \\\\√(n) =(3* 6.5)/(1.3)} \\\\n=((3* 6.5)/(1.3)})^2`

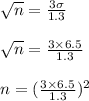
hence,

n = 255