a. Salt flows into tank A at a rate of
(y(t)/500 lb/gal) * (50 gal/min) = y(t)/10 lb/gal
and out at a rate of
(x(t)/500 lb/gal) * (50 gal/min) = x(t)/10 lb/gal
so the net rate of change of the amount of salt in tank A is
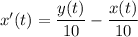
Similarly, you would find

b. We have
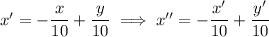
Notice that x' = -y', so

Solve for x: the characteristic equation
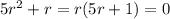
has roots
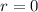 and
and
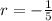 , so
, so
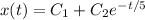
Again using the fact that y' = -x', we then find
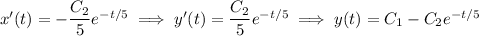
Given that x(0) = 0 and y(0) = 10, we find
