Answer:
a=3
Explanation:
Intersecting Secants Theorem
If two secant segments are drawn to a circle from an exterior point, then the product of the measures of one secant segment and its external secant segment is equal to the product of the measures of the other secant segment and its external secant segment.
Applying the theorem of Intersecting Secants in the diagram
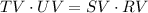
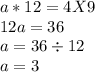
Therefore, the value of a=3