Answer:
The value of m is
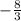 .
.
Explanation:
If two vectors
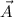 and
and
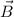 are perpendicular to each other then their dot product will be zero i.e
are perpendicular to each other then their dot product will be zero i.e
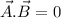
If two vectors
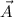 and
and
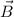 are parallel to each other then their cross product will be zero i.e
are parallel to each other then their cross product will be zero i.e
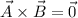
Given vectors are a= (3,4) and b=(m,2)
The position vector of
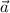 is =
is =
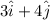
The position vector of
 is =
is =
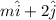
Since
 and
and
 are perpendicular.
are perpendicular.
Then,
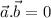
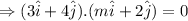
⇒3.m +4.2=0
⇒3m+8=0
⇒3m= -8
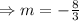
The value of m is
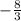 .
.