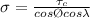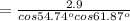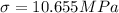Complete Question
Consider a single crystal of some hypothetical metal that has the BCC crystal structure and is oriented such that a tensile stress is applied along a [121] direction. If slip occurs on a (101) plane and in a [111] direction, compute the stress at which the crystal yields if its critical resolved shear stress is 2.9 MPa.
Answer:
The stress is
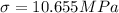
Step-by-step explanation:
From the question we are told that
The critical yield resolved shear stress is
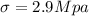
First we obtain the angle
 between the slip direction [121] and [111]
between the slip direction [121] and [111]
![\lambda = cos^(-1) [((u_1 u_2 + v_1 v_2 + w_1 w_2)/(√(u_1^2 + v_1 ^2+ w_1^2))√(( u_2^2 + v_2^2 + w_2 ^2)) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/ko3nl7ti505rl1vjckm377ftyn2nfy3uyw.png)
Where
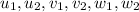 are the directional indices
are the directional indices
![\lambda = cos ^-[ ((1) (-1) + (2) (1) + (1) (1))/(√(((1)^2 +(2)^2 + (1)^2))√(((-1)^2 + (1)^2 + (1)^2 ) ) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/ljxv9jdbokj05sdti0r24vh418borr8zzn.png)
![= cos^(-1) [(2)/(√(6) √(3) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/8fg1fusfx7j28rplv5g9k45ncvf9qqiima.png)
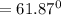
Next is to obtain the angle
 between the direction [121] and [101]
between the direction [121] and [101]
![\O = cos^(-1) [((u_1 u_3 + v_1 v_3 + w_1 w_3)/(√(u_1^2 + v_1 ^2+ w_1^2))√(( u_3^2 + v_3^2 + w_3 ^2)) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/uwhg6iclhsm3vwoi40m6clj7stprd9eepe.png)
Substituting 1 for
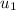 , 2 for
, 2 for
 , 1 for
, 1 for
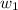 , 1 for
, 1 for
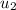 , 0 for
, 0 for
 , and 1 for
, and 1 for

![\O = cos^(-1) [(1* 1 + 2*0 + 1*1 )/(√(1^2 + 2^2 + 1^2 ) √((1^2 + 0^2 + 1^2 )) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/jrpfepz4hhhu06onuqwfs4n7maadbsc1z4.png)
![\O = cos^(-1) [(2)/(√(6) √(2) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/yj30tebgzg2w8qhdryadvngmc8bbk39ipl.png)
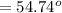
The stress is mathematically represented as