Answer:
The sample size needed to be taken is approximately 74.
Explanation:
To get alpha; we have 1 - 0.95 = 0.05
Therefore,
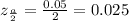
The we look up z* in a Standard Normal table where α = 0.025 area in each tail.
From the table, z* = 1.96
From the question variance is 484, then the standard deviation is 22
Standard deviation =
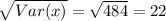
And margin of error is 5 or less
The formula for margin of error is given as:
margin of error =

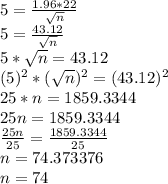
The approximate value of n is 74.