Question:
Parallelogram f"g"h"j" is the final image after the rule ry-axis • t1,2(x, y) was applied to parallelogram fghj. The coordinates are f''(3,4), g''(2,2), h''(4,2) and j''(5,4)
what are the coordinates of vertex f of parallelogram fghj?
(–2, 2)
(–2, 6)
(–3, 4)
(–4, 2)
Given:
Given that the the coordinates of the parallelogram f''g''h''j'' is the final image after the rule ry-axis • t1,2(x, y) was applied to parallelogram fghj.
The coordinates are f''(3,4), g''(2,2), h''(4,2) and j''(5,4)
We need to determine the coordinates of vertex f of parallelogram fghj.
Reflection across y - axis:
The general rule to reflect the coordinate across y - axis is given by
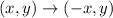
Substituting the coordinate f''(3,4), we get;
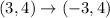
Thus, the coordinates of f'' of reflection across the y - axis is (-3,4)
Translation T1,2(x, y):
The translation can be performed using the rule,
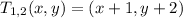
Now, substituting the coordinate (-3,4), we get;
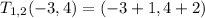
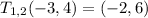
Thus, the coordinates of vertex F is (-2,6)
Hence, Option b is the correct answer.