Question

Researchers are studying two populations of sea turtles. In population D, 30 percent of the turtles have a shell length greater than 2 feet. In population E, 20 percent of the turtles have a shell length greater than 2 feet. From a random sample of 40 turtles selected from D, 15 had a shell length greater than 2 feet. From a random sample of 60 turtles selected from E, 11 had a shell length greater than 2 feet. Let pˆD represent the sample proportion for D, and let pˆE represent the sample proportion for E.

(a) What is the value of the difference pˆD−pˆE? Show your work.

Answer 1

`p^D-p^E=0.192`

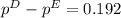
Explanation:

We are given the following in the question:

Population D:

30% of the turtles have a shell length greater than 2 feet.

Sample size,

`n_D = 40`

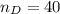
Number of turtles that had shell length greater than 2 feet,

`x_D = 15`

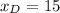
Sample proportion:

`p^D=(x_D)/(n_D) =(15)/(40) = 0.375`

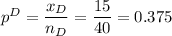
Population E:

20% of the turtles have a shell length greater than 2 feet.

Sample size,

`n_E = 60`

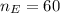
Number of turtles that had shell length greater than 2 feet,

`x_E = 11`

Sample proportion:

`p^E=(x_E)/(n_E) =(11)/(60) = 0.183`

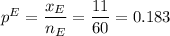
We have to find the difference between the sample proportion.

Difference in sample proportion =

`=p^D-p^E\\=0.375-0.183\\=0.192`