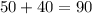Question

Dado dos ángulos complementarios, uno mide (2x + 10) y el otro (x + 20),

calcula el valor de x​

Answer 1

El valor de x es igual a 20 o x = 20.

Explanation:

Lo primero que se debe saber es que dos ángulos complementarios suman un ángulo recto o 90º.

Supongamos que el valor de un ángulo
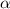`\\ \alpha` y un ángulo
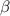`\\ \beta` valen:

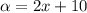`\\ \alpha = 2x + 10` [1]

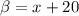`\\ \beta = x + 20` [2]

Como la suma de
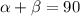`\\ \alpha + \beta = 90` [3]

Entonces

`\\ \alpha + \beta = (2x + 10) + (x + 20) = 90`

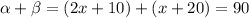
Sumamos los factores comunes entre si:

`\\ (2x + x) + (10 + 20) = 90`

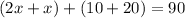
Para la primera expresión debemos recordar que se suman sólo los coeficientes. Así:

`\\ (2 + 1)x + (10 + 20) = 90`

`\\ 3x + 30 = 90`

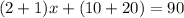
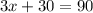
Para despejar la incógnita x, debemos tener en cuenta que una igualdad no se altera si se suma, se resta, se multiplica o divide un mismo valor a cada lado de ella. Por esta razón, para despejar 3x, lo primero que podemos hacer es sumar -30 a cada lado de la expresión (lo que es igual a restar 30 a cada lado de la misma). Así tenemos:

`\\ 3x + 30 - 30 = 90 - 30`

`\\ 3x + 0 = 90 - 30`

`\\ 3x = 60`

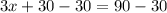
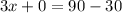
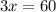
Ahora dividimos cada miembro de la igualdad entre 3 (o multiplicamos cada lado de la igualdad por
`\\ (1)/(3)` ):

`\\ (3)/(3)x = (60)/(3)`

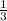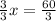
Como sabemos que:

`\\ (3)/(3) = 1`

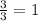
Entonces:

`\\ 1*x = (60)/(3)`

`\\ x = (60)/(3)`

`\\ x = 20`

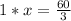
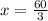
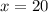
De esta manera, el valor de x es igual a 20 o x = 20.

Lo anterior lo podemos comprobar considerando las ecuaciones [1], [2] y [3]. Así tenemos que:

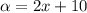`\\ \alpha = 2x + 10` [1]

Sustituimos x por el valor de 20:

`\\ \alpha = 2*20 + 10 = 40 + 10 = 50`

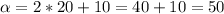
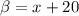`\\ \beta = x + 20` [2]

Hacemos lo mismo para [2]:

`\\ \beta = 20 + 20`

`\\ \beta = 40`

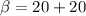
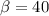
De esta manera:

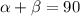`\\ \alpha + \beta = 90` [3]

`\\ 50 + 40 = 90`