Answer:
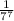 ≈
≈
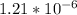
Explanation:
Our equation is
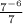 . Whenever we have a negative exponent, we can turn it positive by moving it from the numerator to the denominator or vice versa (depending on where it's located). Here, 7^(-6) is in the numerator so we can then move it to the denominator and make it positive:
. Whenever we have a negative exponent, we can turn it positive by moving it from the numerator to the denominator or vice versa (depending on where it's located). Here, 7^(-6) is in the numerator so we can then move it to the denominator and make it positive:

Remember that when multiplying powers with the same base (in this case, that shared base is 7), we can combine them into one by adding the exponents. Here, we have 7^6 (exponent is 6) and 7 (exponent is 1). So:
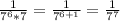
If we want to find the decimal expansion of this, it is around:
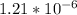 (in scientific notation).
(in scientific notation).
Hope this helps!