Question

The height of the tide in a small beach town is measured along a seawall. Water levels oscillate between 7 feet at low tide and 15 feet at high tide. On a particular day, low tide occurred at 7:30 AM and high tide occurred at 1:00 PM.

Answer 1

Question:

Write a cosine function of the form f(t)= Acos(Bt) where A and B are real numbers that models the water level f(t) as a function of time measured in t hours since 8:30 a.m.

Answer:

The equation of the cosine function that models the water level as a function of time is;

`f(t) = -4* cos((2\pi )/(13) t)`

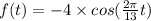
Explanation:

From the required equation, we have for a wave form

f(t) = A·cos(B·t)

A = Amplitude of the wave

B = The period of the wave

t = Time of wave

The period can be derived as follows

We have 7:30 to 1:00 is 5.5 hrs, therefore one full cycle occurs in 11 hours

The period is given by;

`Period = (2\pi )/(B)`

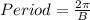
Therefore,

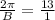`(2\pi )/(B) = (13)/(1)` so that

`The \, period \, B = (2\pi )/(13)`

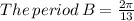
The amplitude is given as the maximum displacement from the position at rest. Therefore, the amplitude = (15 - 7)/2 = 4 feet

Therefore the equation of the cosine function that models the water level as a function of time is;

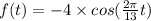`f(t) = -4* cos((2\pi )/(13) t)`.