Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The angular acceleration for first drum
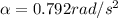
The angular acceleration for the second drum is

Step-by-step explanation:
From the question we are told that
Their radius of the drum is
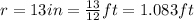 each
each
The weight is

The mass is
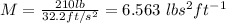
Their radius of gyration is
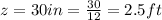
The free body diagram of a drum and its hub and 30lb and in the case the weight is connect to the hub separately is shown on the second uploaded image
The T in the diagram is the tension of the string
Now taking moment about the center of the the drum P we have
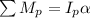
=>
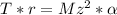
Where r is the radius ,z is the radius of gyration about the center O , M is the mass of the drum including the hub, and
 is the angular acceleration
is the angular acceleration
Inputting
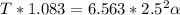
=>
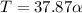
Considering the force equilibrium in the vertical direction (Looking at the second free body diagram now )
The first on is

=>
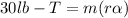
Where m is the mass of the hanging block which has a value of
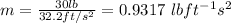
a is the acceleration of the hanging block
inputting values we have

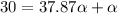
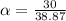
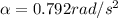
So the angular acceleration for first drum
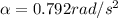
The free body diagram of a drum and its hub when the only on the string is 30lb is shown on the third uploaded image
So here we would take the moment about O
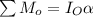
So
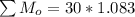
and
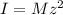
Therefore we will have
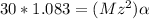
inputting values
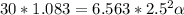

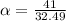

So the angular acceleration for the second drum is
