Question

The lifespans of zebras in a particular zoo are normally distributed. The average zebra lives 20.5years; the standard deviation is 3.9 years. Use the empirical rule (68-95-99.7%)to estimate the probability of a zebra living less than 32.2 years.

Answer 1

Answer: 68, if the question asks between 16.6 and 24.4 years. 99.85, if the question asks for less.

Explanation:

Answer 2

Using the empirical rule, the probability of a zebra living less than 32.2 years is about
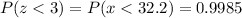`\\ P(z<3) = P(x<32.2) = 0.9985` or about 99.85%.

Step-by-step explanation:

Roughly speaking, the empirical rule tells us that, in a normal distribution, the distance of one standard deviation from the mean, above and below it, contains approximately 68% of the observations of the normally distributed data; two standard deviations from the mean, above and below it, 95% of the data, and, finally, the distance of three standard deviations from the mean, above and below it, contains 99.7% of the data, approximately.

To estimate probabilities with this rule, we need to use, at least, two concepts: the standard normal distribution and the z-scores. A standard normal distribution is a normal distribution with mean = 0 and standard deviation = 1. It represents standardized data. This standardized data are those coming from a normal distribution and commonly called raw data. The way to standardized them is using the z-scores:

`\\ z = (x - \mu)/(\sigma)` [1]

Where

x represents raw data. In this case, x = 32.2 years.

`\\ \mu` is the population mean. In this case,
`\\ \mu = 20.5` years.

`\\ \sigma` is the population standard deviation. In this case,
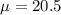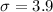`\\ \sigma = 3.9` years.

Then, using [1], we "transform" the raw score into a z-score (a standardized value) and then use this to find the corresponding probability using the standard normal distribution (or the cumulative standard normal distribution to be more precise), available in any Statistics book or on the Internet.

However, applying the empirical rule, we can estimate those probabilities faster but in an approximate way.

Let us take the corresponding z-score:

`\\ z = (x - \mu)/(\sigma)`

`\\ z = (32.2 - 20.5)/(3.9)`

`\\ z = (11.7)/(3.9)`

`\\ z = 3`

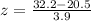
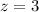
That is, the value z = 3 tells us the raw score 32.2 years is three standard deviations from the mean. In other words, 99.7% of the values are between z = -3 and z = 3. However, we are asked for P(z<3). The remaining area is below z = -3 and above z = 3. Since the normal distribution is symmetrical, we have to divide the remaining area by 2. That is, (1 - 0.997)/2 = 0.003/2 = 0.0015.

The area below z = -3 is, therefore, 0.0015, as well as above z = 3 or P(z<-3) = P(z>3) = 0.0015. The only area that not correspond to P(z<3) is P(z>3). As a result, we need to add the area below z = -3 (0.0015) to the value of 0.997 to finally have P(z<3).

Then

`\\ P(z<3) = P(x<32.2) = 0.997 + P(z<-3)`

`\\ P(z<3) = P(x<32.2) = 0.997 + 0.0015`

`\\ P(z<3) = P(x<32.2) = 0.9985`

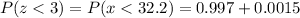
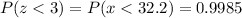
Thus, using the empirical rule, the probability of a zebra living less than 32.2 years is about
`\\ P(z<3) = P(x<32.2) = 0.9985`.

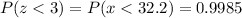In the graph below, we have a representation of the area below z = 3 or P(z<3) = P(x<32.2) is, approximately, 0.9985 or 99.85%.

Notice that using the cumulative standard normal table, as explained before, we have that P(z<3) = 0.99865.