Answer:
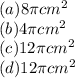
Explanation:
Radius of the Sphere =2cm
(a)Surface Area of the rounded part of the Hemisphere
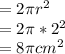
(b)Area of the circular base of the hemisphere
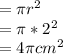
(c)Total Surface Area =Area of the rounded part+Area of the circular base
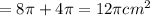
(d)If another student completed the same problem using the formula,
Surface Area of a Hemisphere
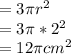
The solution would be the same as the surface area determined above.