Question

Find the vertices and foci of the hyperbola with equation quantity x plus 2 squared divided by 144 minus the quantity of y minus 4 squared divided by 81 = 1.

Answer 1

• Vertices:(-14,4) and (10,4).
• Foci: (–17, 4) and (13, 4)

Explanation:

Given the equation of the hyperbola

`((x+2)^2)/(144)-((y-4)^2)/(81) =1`

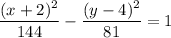
Since the x part is added, then

`a^2=144; b^2=81\\a=12,b=9`

Also, this hyperbola's foci and vertices are to the left and right of the center, on a horizontal line paralleling the x-axis.

From the equation, clearly the center is at (h, k) = (–2, 4). Since the vertices are a = 12 units to either side, then they are at (-14,4) and (10,4).

From the equation

`c^2=a^2+b^2=144+81=225\\c=15`

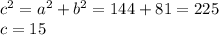
The foci, being 15 units to either side of the center, must be at (–17, 4) and (13, 4)