Answer:
7.54 x
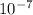 C
C
Step-by-step explanation:
The complete question is:
Students in an introductory physics lab are performing an experiment with a parallel-plate capacitor made of two circular aluminum plates, each 19 cm in diameter, separated by 1.0 cm.How much charge can be added to each of the plates before a spark jumps between the two plates? For such flat electrodes, assume that value of 3×106N/C of the field causes a spark.
SOLUTION:
As you know that, parallel plate capacitance can be defined as
C=εo A/d
Where,
εo is the permittivity of free space constant, A is area of the capacitor plates, and d is the distance between them
Also, C= Q/V
where,
'Q' defines charge stored on the capacitor and 'V' express the potential difference between the plates.
Equating the equations.
εo A/d = Q/V
Q= (εo A V)/d
for a uniform electric field (such as the one between the plates of a parallel-plate capacitor)
V= Ed ->where 'E' defines magnitude of the electric field.
Therefore,
Q= (εo A E d)/d =>εo A E ->eq(1)
The area of the plates is given by
A= πr² => π(d/2)² =>π(0.19/2)
A=0.0284m²
Given: E= 3 x
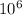 N/C
N/C
Substituting all the required values in eq(1)
(1)=> Q= (8.85x
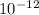 ) (-.0284)(3 x
) (-.0284)(3 x
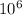 )
)
Q= 7.54 x
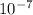 C
C
Therefore,7.54 x
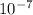 C can be added to each of the plates before a spark jumps between the two plates
C can be added to each of the plates before a spark jumps between the two plates