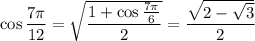2 Answers

Smitelli · Answer 1 · 2021-07-31T06:04:46+0000

I suppose x should be π.

Recall the double angle identity for cosine:

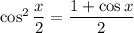
$\cos^2\frac x2=\frac{1+\cos x}2$

Then remember for
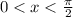$0<x<\frac\pi2$ , we have
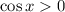$\cos x>0$ .

Let
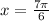$x=\frac{7\pi}6$ . Plugging this into the equation above gives

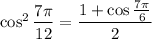
$\cos^2(7\pi)/(12)=\frac{1+\cos\frac{7\pi}6}2$

Take the square root of both sides; this introduces two possible values, but we know
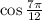$\cos(7\pi)/(12)$ should be positive, so

$\cos(7\pi)/(12)=\sqrt{\frac{1+\cos\frac{7\pi}6}2}=\frac{√(2-\sqrt3)}2$

Please log in or register to add a comment.