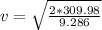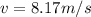Question

While a roofer is working on a roof that slants at 37.0 ∘∘ above the horizontal, he accidentally nudges his 92.0 NN toolbox, causing it to start sliding downward, starting from rest. If it starts 4.25 m from the lower edge of the roof, how fast will the toolbox be moving just as it reaches the edge of the roof if the kinetic friction force on it is 22.0 N?

Answer 1

The speed is
`v =8.17 m/s`

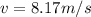
Step-by-step explanation:

From the question we are told that

The angle of slant is
`\theta = 37.0^o`

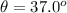
The weight of the toolbox is
`W_t = 92.0N`

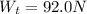
The mass of the toolbox is
`m = (92)/(9.8) = 9.286kg`

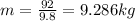
The start point is
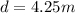`d = 4.25m` from lower edge of roof

The kinetic frictional force is
`F_f = 22.0N`

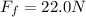
Generally the net work done on this tool box can be mathematically represented as

`Net \ work done = Workdone \ due \ to \ Weight + Workdone \ due \ to \ Friction`

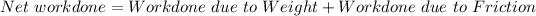
The workdone due to weigh is =
`mgsin \theta * d`

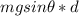
The workdone due to friction is =
`F_f \ cos\theta * d`

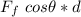
Substituting this into the equation for net workdone

`W_(net) = mgsin\theta * d + F_f \ cos \theta *d`

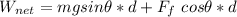
Substituting values

`W_(net) = 92 * sin (37) * 4.25 + 22 cos (37) * 4.25`

`= 309.98 J`

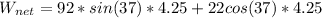
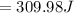
According to work energy theorem

`W_(net) = \Delta Kinetic \ Energy`

`W_(net) = (1)/(2) m (v - u)^2`

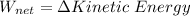
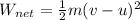
From the question we are told that it started from rest so u = 0 m/s

`W_(net) = (1)/(2) * m v^2`

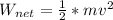
Making v the subject

`v = \sqrt{(2 W_(net))/(m) }`

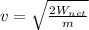
Substituting value

`v = \sqrt{(2 * 309.98)/(9.286) }`

`v =8.17 m/s`