Question

If VX=15 and WX=7, what is UX? Write your answer as a whole number, improper fraction, or as a decimal rounded to the nearest hundredth.

Answer 1

Given:

Given that the length of VX is 15.

The length of WX is 7.

We need to determine the altitude UX of the given triangle.

Altitude UX:

The value of the altitude UX can be determined using the altitude rule theorem.

Applying the theorem, we have;

`(left)/(altitude)=(altitude)/(right)`

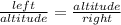
Substituting left = UX, altitude = VX and right = VW in the above formula, we get;

`(UX)/(VX)=(VX)/(XW)`

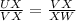
Substituting the values, we get;

`(UX)/(15)=(15)/(7)`

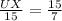
Multiplying both sides of the equation by 15, we have;

`UX=(15 * 15)/(7)`

`UX=(225)/(7)`

`UX=32.14`

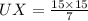
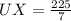
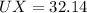
Thus, the length of UX is 32.14 units.