Question

Write a polynomial f(x) that satisfies the given conditions.

Polynomial of lowest degree with zeros of

(multiplicity 2) and

(multiplicity 1) and with f(0) = -1.

Can someone do this?

Answer 1

`f(x) = (x-4)(x-(1)/(2))^2 = x^3-5x^2+4.25x -1`

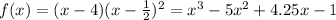
Explanation:

Recall, if we have a polynomial of the form
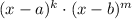`(x-a)^k \cdot (x-b)^m`, then we say that a is a zero of multiplicity k and b is a zero of multiplicty m. For example, in the polynomial of the form
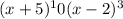`(x+5)^10(x-2)^3` -5 is a zero of multiplicity 10 and 2 is a zero of multiplicity 3. If we want to know the degree of the polynomial, just add the multiplicity of both zeros (13 in our example).

In this case, we know that the degree of our polynomial should be at least 3(multiplicity 2 and multiplicity 1). So, lets take the polynomial of the form

`f(x)=(x-a)(x-b)^2)`.

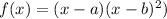In here, a is a zero with multiplicity 1 and b is a zero with multiplicity 2. We are also given that

`f(0) = -1 = (0-a)(0-b)^2 = -a\codt b^2`.

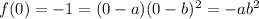Which implies that
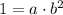`1 = a\cdot b^2`. Since the square of any number is a positive number, it must happen that a>0. So, we have that

`b= \pm \sqrt[]{(1)/(a)}`.

We can choose any value of a and solve for b. Let us choose a=4. So we can have b=1/2 or b=-1/2. Let's use b=1/2. So our polynomial would be

`f(x) = (x-4)(x-(1)/(2))^2 = x^3-5x^2+4.25x -1`

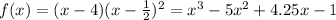
which we can easily check that f(0)=-1.