Question

Help please, asap
50 points

Answer 1

The answer is shown in the picture☝️.

Formula :

cos(π/2 - x) = sin x

cos(π - x) = -cos x

cos²x + sin²x = 1

loga(b) + loga(c) = loga(b×c)

Answer 2

Steps to solve:

5 - 5cos(π/2 - x) = 2cos²(π - x)

~Use an identity to simplify cos(π/2 - x)

cos(π/2 - x) → sin(x)

~Use an identity to simplify cos(π - x)

cos(π - x) → -cos(x)

~Put back into an expression

5 - 5sin(x) = 2(-cos(x))²

~Simplify

5 - 5sin(x) = 2cos²(x)

~Subtract 2cos²(x) to both sides

5 - 5sin(x) - 2cos²(x) = 2cos²(x) - 2cos²(x)

~Simplify

5 - 5sin(x) - 2cos²(x) = 0

~Use an identity to simplify

5 - (1 - sin²(x)) * 2 - 5sin(x) = 0

~Simplify

3 + 2sin²(x) - 5sin(x) = 0

~Let sin(x) = u

3 + 2u² - 5u = 0

~Use the quadratic formula to solve for u.

`x=(-(-5)+-√((-5)^2-4(2)(3)) )/(2(2))`

`u = (3)/(2), u=1`

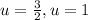
~Substitute back with sin(x) = u

sin(x) = 3/2 or sin(x) = 1

Steps to solve:

log₂(1 - x) + log₂(-5x - 2) = 2 + log₂3

~Apply log rule

log₂((1 - x(-5x - 2)) = 2^2+(log₂(3)

~Use log definition

(1 - x)(-5x - 2) = 2^2+log₂(3)

~Expand both sides

5x² - 3x - 2 = 12

~Subtract 12 to both sides

5x² - 3x - 2 - 12 = 12 - 12

~Simplify

5x² - 3x - 14 = 0

~Use the quadratic formula to solve

`x = (-(-3)+-√((-3)^2-4(5)(-14)) )/(2(5))`

~Simplify

x = 2 or x = -7/5

Best of Luck!