Answer:
Minimum 7 buckets of water is needed to completely fill spherical storage tank.
Explanation:
We are given the following in the question:
Cylindrical bucket:
Radius, r = 6 inches
Height = 18 inches
Volume of bucket = Volume of cylinder
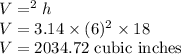
Spherical storage tank:
Radius, r = 15 inches
Volume of tank = Volume of sphere =
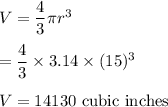
Number of baskets required =
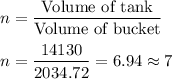
Thus, minimum 7 buckets of water is needed to completely fill spherical storage tank.