Question

When 3010 adults were surveyed in a poll, 22% said that they use the Internet. Is it okay for a newspaper reporter to write that "1/4 of all adults use the

Interer? Why or why not? Identify the null hypothesis, alternative hypothesis, test statistic, P-value, conclusion about the null hypothesis, and final conclusion
that addresses the original claim. Use the P-value method. Use the normal distribution as an approximation of the binomial distribution
Identify the null and alternative hypotheses. Choose the correct answer below.

Answer 1

Hypotheses:

H₀: p = .25

Hₐ: p ≠ .25

Conditions:

• Random sample NOT stated -- proceed with caution!
• Normality: 3010(.22) = 662.2 ≥ 10 and 3010(1 - .22) = 2347.8 ≥ 10
• Independence: 3010(10) = 30100 < all adults (reasonable to assume)

Test statistic:

`\displaystyle z = \frac{.22-.25}{\sqrt{((.25)(.75))/(3010) } } \\ \\ \\ z = (-.03)/(.00789) \\ \\ \\ \boxed{z = -3.8011}`

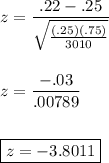
Conduct the two-tailed test to calculate the area corresponding to the positive and negative z-score.

• The p-value for the lower tail is .00007205. Multiply this by two to get the area for both tails:
• p = .0001441

Conclusion:

Since p = .0001441 < α = .05, we reject the null hypothesis. There is convincing statistical evidence that the true proportion of adults that use the internet is not equal to .25.