Question

In 2012, Gallup asked participants if they had exercised more than 30 minutes a day for three days out of the week. Suppose that random samples of 100 respondents were selected from both Vermont and Hawaii. From the survey, Vermont had 65.3% who said yes and Hawaii had 62.2% who said yes. What is the value of the population proportion of people from Vermont who exercised for at least 30 minutes a day 3 days a week?

Answer 1

The estimated population proportion of Vermont residents who exercised for at least 30 minutes a day 3 days a week is 65.3%, which is based on the sample proportion from the Gallup survey.

Step-by-step explanation:

The student is asking about the population proportion for people from Vermont who exercised for at least 30 minutes a day 3 days a week based on the Gallup survey results. The survey indicated that 65.3% of the Vermont respondents exercised at the mentioned rate.

To find the value of the population proportion (population proportion), we typically use the sample proportion as an estimate. From the survey, we have that the sample proportion (p-hat) for Vermont is 65.3%, which we express as a decimal, 0.653. Assuming the sample is representative, we would estimate the population proportion to also be 0.653 or 65.3%.

It's important to note that this is an estimate based on the sample and that to infer more confidently about the entire population of Vermont, a larger sample size or additional statistical methods such as confidence intervals or hypothesis testing may be applied. Nevertheless, with the information provided, the best estimate for the population proportion of Vermont residents who exercised according to the guidelines is the sample proportion of 65.3%.

Answer 2

There is 95% confidence that the population proportion of people from Vermont who exercised for at least 30 minutes a day 3 days a week is between 55.9% and 74.7%.

Step-by-step explanation:

We have to answer the population proportion for Vermont.

We can only do it by a confidence interval, as we only have information from a sample.

This sample, of size n=100, has a proportion p=0.653.

The degrees of freedom are:

`df=n-1=100-1=99`

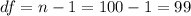
We will calculate a 95% confidence interval, which for df=99 has a critical value of t of t=1.984.

The margin of error can be calculated as:

`E=t*\sigma_p=t\sqrt{(p(1-p))/(n)}=1.984\sqrt{(0.653*0.347)/(100)}\\\\\\E=1.984*√(0.00226)=1.984*0.0476=0.094`

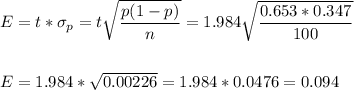
Then, the upper and lower bounds of the confidence interval are:

`LL=p-E=0.653-0.094=0.559\\\\UL=p+E=0.653+0.094=0.747`

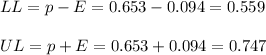
Then, we can say that there is 95% confidence that the population proportion of people from Vermont who exercised for at least 30 minutes a day 3 days a week is between 55.9% and 74.7%.