Answer:
781250 Square Meters
Explanation:
Let the dimensions of the rectangular plot be x and y
Farmer Ed wants to enclose three sides of a rectangular plot with a fencing of 2500 meters.
Therefore: Perimeter, P=x+2y=2500
We want to find the largest area that can be enclosed.
Area of the plot, A(x,y)=xy
Substitute x=2500-2y
A(y)=(2500-2y)y
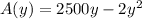
To maximize A, we first find its derivative

The largest area that can be enclosed(at x=1250m,y=625m) is:
1250 X 625
=781250 Square Meters