The x-coordinate of point A, situated in the third quadrant on the unit circle with an angle of
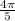 , is
, is
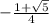 .
.
The x-coordinate of a point on the unit circle in the third quadrant can be found using the cosine function. In this case, since the angle
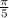 is measured counterclockwise from the positive x-axis, the x-coordinate is given by:
is measured counterclockwise from the positive x-axis, the x-coordinate is given by:
![\[ \text{x-coordinate of A} = \cos\left(\pi - (\pi)/(5)\right) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/98co4jj37c0039m1uv83fhmdf34b0a0e37.png)
Simplifying the expression inside the cosine function:
![\[ \text{x-coordinate of A} = \cos\left((4\pi)/(5)\right) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/b21m2pjhgxgy2evgq4jwbzzhttf7u7jlds.png)
Now, evaluate the cosine of
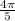 :
:
![\[ \text{x-coordinate of A} = \cos\left((4\pi)/(5)\right) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/b21m2pjhgxgy2evgq4jwbzzhttf7u7jlds.png)
Without numerical calculation, we know that
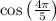 is negative because
is negative because
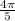 is in the second quadrant. Therefore, the x-coordinate of point A is negative.
is in the second quadrant. Therefore, the x-coordinate of point A is negative.
Let's evaluate the cosine of
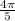 :
:
![\[ \text{x-coordinate of A} = \cos\left((4\pi)/(5)\right) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/b21m2pjhgxgy2evgq4jwbzzhttf7u7jlds.png)
Cosine values for special angles can be determined without a calculator. The angle
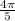 corresponds to a
corresponds to a
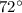 angle in degrees. In the unit circle, cosine is negative in the second quadrant.
angle in degrees. In the unit circle, cosine is negative in the second quadrant.
So,
 .
.
Using known values:
![\[ \cos(72^\circ) = (1 + √(5))/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/z6b18uhg4rfmmacbqn7wk5vzdjl3gndjei.png)
Therefore,
![\[ \text{x-coordinate of A} = -(1 + √(5))/(4) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/y9ny86xfm5i6f7wa0vddwe1eshpf1q68yb.png)
This is the exact value of the x-coordinate of point A.