Question

he Faulk Corp. has a bond with a coupon rate of 4 percent outstanding. The Yoo Company has a bond with a coupon rate of 10 percent outstanding. Both bonds have 17 years to maturity, make semiannual payments, and have a YTM of 7 percent. If interest rates suddenly rise by 2 percent, what is the percentage change in the price of these bonds

Answer 1

Faulk: -0,1925629 = -19.25%

Yoo: 0,1615398 = 16.15%

Step-by-step explanation:

We need to solve forthe present value of the coupon and maturity on each bond considering the yield to maturity of 7% and 9% and compare the price variations:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 20.000

time 34

rate 0.035

`20 * (1-(1+0.035)^(-34) )/(0.035) = PV\\`

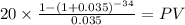
PV $394.0137

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 34.00

rate 0.035

`(1000)/((1 + 0.035)^(34) ) = PV`

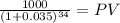
PV 310.48

PV c $394.0137

PV m $310.4761

Total $704.4897

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 20.000

time 34

rate 0.045

`20 * (1-(1+0.045)^(-34) )/(0.045) = PV\\`

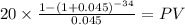
PV $344.9352

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 34.00

rate 0.045

`(1000)/((1 + 0.045)^(34) ) = PV`

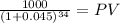
PV 223.90

PV c $344.9352

PV m $223.8959

Total $568.8311

Price variation on Faulk

($568.8311 - $704.4897) / $704.4897 = -0,1925629

Yoo Company:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 50.000

time 34

rate 0.035

`50 * (1-(1+0.035)^(-34) )/(0.035) = PV\\`

PV $985.0342

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 34.00

rate 0.035

`(1000)/((1 + 0.035)^(34) ) = PV`

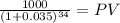
PV 310.48

PV c $985.0342

PV m $310.4761

Total $1,295.5103

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 50.000

time 34

rate 0.045

`50 * (1-(1+0.045)^(-34) )/(0.045) = PV\\`

PV $862.3379

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 34.00

rate 0.045

`(1000)/((1 + 0.045)^(34) ) = PV`

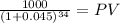
PV 223.90

PV c $862.3379

PV m $223.8959

Total $1,086.2338

($1,295.5103 - $1,086.2338 ) / $1,295.5103 = 0,1615398