Ina city school, 65% of students have green eyes. 25% have red hair, and 15% have green eyes and red hair. What is the probability (rounded to the nearest whole percent) that a …

Question

asked May 16, 2021 1.8k views

1 Answer

Qts · Answer 1 · 2021-05-22T10:55:01+0000

Answer:

23% of student will have red hair given that the student has green eyes.

Explanation:

We are given the following in the question:

Percentage of students that have green eyes = 65%

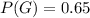
P(G) =0.65

Percentage of students that have red hairs = 25%

P(R) =0.25

Percentage of students that have green eyes and red hairs = 15%

$P(G\cap R) =0.15$

We have to find the conditional probability of randomly selected student that will have red hair given that the student has green eyes.

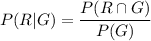
$P(R|G) = (P(R\cap G))/(P(G))$

Putting values, we get,

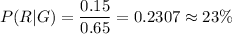
$P(R|G)=(0.15)/(0.65) = 0.2307\approx 23\%$

Thus, 23% of student will have red hair given that the student has green eyes.