Question

two high school students took equivalent language tests, one in German and one in French. The student taking the German test, for which the mean was 66 and the standard deviation was 8, scired ab 82, while the student taking the French test, for which the mean was 27 and the standard deviation was 5, scored a 35. Compare the scores.

Answer 1

The student who did the German test scored 2 standard deviations above the mean and the student who did the French test scored 1.6 standard deviations above the mean. Relative to their classmates, the student who did the German test scored better due to the higher z-score.

Explanation:

Z-score

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

German test

Mean was 66 and the standard deviation was 8, scored an 82.

So

`Z = (X - \mu)/(\sigma)`

`Z = (82 - 66)/(8)`

`Z = 2`

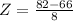
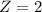
French test:

Mean was 27 and the standard deviation was 5, scored a 35.

So

`Z = (X - \mu)/(\sigma)`

`Z = (35 - 27)/(5)`

`Z = 1.6`

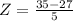
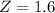
The student who did the German test scored 2 standard deviations above the mean and the student who did the French test scored 1.6 standard deviations above the mean. Relative to their classmates, the student who did the German test scored better due to the higher z-score.