Answer:
Cov (X,Y) = 6
Explanation:
hello,
Cov(X,Y) = E(XY) - E(X)E(Y)
we must first find E(XY), E(X), and E(Y).
since X is uniformly distributed on the interval (0,12), then E(X) = 6.
next we find the joint density f(x,y) using the formula
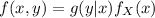
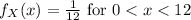 this is because f is uniformly distributed on the the interval (0,12)
this is because f is uniformly distributed on the the interval (0,12)
also since the conditional probability density of Y given X=x, is uniformly distributed on the interval [0,x], then
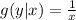 for 0≤y≤x≤12
for 0≤y≤x≤12
thus
 .
.
hence,
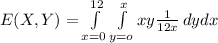
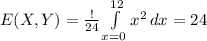
also,
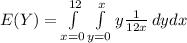
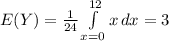
thus Cov(X,Y) = E(XY) - E(X)E(Y)
= 24 - (6)(3)
= 6