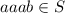Question

Let S be the set of all strings from A* in which there is no b before an a. For example, the strings λ, aa, bbb, and aabbbb all belong to S, but aabab ∉ S. Give a recursive definition for the set S. (Hint: a recursive rule can concatenate characters at the beginning or the end of a string.)

Answer 1

Check the explanation

Step-by-step explanation:

A recurvsive defintion for
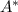`A^(*)` which contains all possible strings over the alphabet
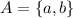`A=\{a,b\}`is \lambda\in
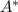`A^*`(contains the null strings) and
`A^(*)=\{uv:u\in A^*,v\in A\}`

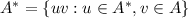
A recurvsive defintion for
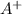`A^(+)` which contains all possible strings over the alphabet
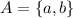`A=\{a,b\}` is
`a,b\in`
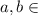
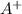`A^+` (contains the strings of lengths 1) and
`A^(+)=\{uv:u\in A^+,v\in A\}`

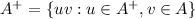
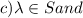
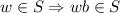
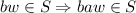`c) \lambda \in S and`

`w\in S\Rightarrow wb \in S`

`bw\in S\Rightarrow baw \in S` and
`awb\in S`

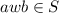
is the required recursive definition for S

For example,
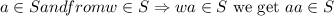`a\in S and from w\in S\Rightarrow wa\in S\text{ we get }aa\in S` also

Again, as
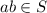`ab\in S`and from
`wb\in S\Rightarrow wab \in S we get aab\in S`

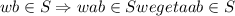
And as
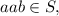`aab\in S,` from
`wb\in S\Rightarrow wab \in S and awb\in S` we have
`aaab\in S`