Hi there!
A.
We can use the work-energy theorem to solve.
Initially, both blocks have gravitational potential energy, which is then converted to kinetic energy.
Recall:
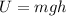
U = Potential Energy (J)
m = mass (kg)
g = acceleration due to gravity (m/s²)
h = height (m)
And at the end, block 2 has both kinetic and potential energy. Kinetic is defined as:
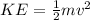
v = velocity (m/s)
We can do a summation of initial and final forces.
Initial:
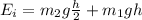
Final:
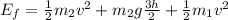
Set the two equal (no energy loss in this situation) and solve for velocity.
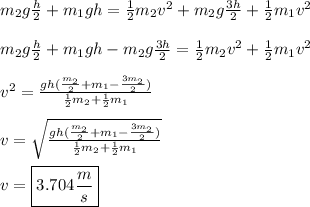
**This can be solved in a simpler way using a summation of forces.
B.
Now, we can do a summation of forces to solve. First, we must solve for the acceleration of the system now that we have found the velocity. Use the kinematic equation:
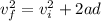
Initial velocity is 0 m/s, so:
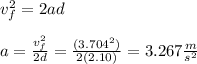
Now, we can use a summation of forces for any block. We can do block 1:
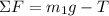
Using Newton's Second Law:
