Answer:
Explanation:
Given Parameters
Mean,
 = 180
= 180
total samples, n = 20
Standard dev,
 = 30
= 30
 = 1 - 0.95 = 0.05 at 95% confidence level
= 1 - 0.95 = 0.05 at 95% confidence level
Df = n - 1 = 20 - 1 = 19
Critical Value,
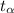 , is given by
, is given by
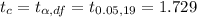
a).
Confidence Interval,
 , is given by the formula
, is given by the formula
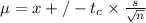
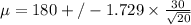
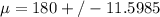
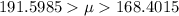
b).
Critical Value,
 , is given by
, is given by
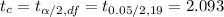
Confidence Interval,
 , is given by
, is given by
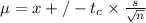
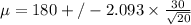
= 180 +/- 14.0403
= 165.9597 <
 < 194.0403
< 194.0403