Question

1. (5.1.8) An article reports that in a sample of 132 hip surgeries of a certain type, the average surgery time was 136.9 minutes with a standard deviation of 22.6 minutes. a. Find a 95% confidence interval for the mean surgery time. b. Find a 99.5% confidence interval for the mean surgery time. c. A surgeon claims that the mean surgery time is between 133.9 and 139.9 minutes. With what level of confidence can this statement be made? d. Approximately how many surgeries must be sampled so that a 95% confidence interval will specify the mean to within ±3 minutes? e. Approximately how many surgeries must be sampled so that a 99% confidence interval will specify the mean to within ±3 minutes?

Answer 1

a) The 95% CI for the mean surgery time is (133.05, 140.75).

b) The 99.5% CI for the mean surgery time is (131.37, 142.43).

c) The level of confidence of the interval (133.9, 139.9) is 69%.

d) The sample size should be 219 surgeries.

e) The sample size should be 377 surgeries.

Explanation:

We have a sample, of size n=132, for which the mean time was 136.9 minutes with a standard deviation of 22.6 minutes.

a) We have to find a 95% CI for the mean surgery time.

The critical value of z for a 95% CI is z=1.96.

The margin of error of the CI can be calculated as:

`E=z\cdot s/√(n)=1.96*22.6/√(132)=44.296/11.489=3.85`

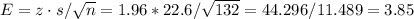
Then, the lower and upper bounds of the confidence interval are:

`LL=\bar x-E=136.9-3.85=133.05\\\\UL=\bar x+E=136.9+3.85=140.75`

The 95% CI for the mean surgery time is (133.05, 140.75).

b) Now, we have to find a 99.5% CI for the mean surgery time.

The critical value of z for a 99.5% CI is z=2.81.

The margin of error of the CI can be calculated as:

`E=z\cdot s/√(n)=2.81*22.6/√(132)=63.506/11.489=5.53`

Then, the lower and upper bounds of the confidence interval are:

`LL=\bar x-E=136.9-5.53=131.37\\\\UL=\bar x+E=136.9+5.53=142.43`

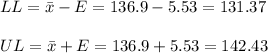
The 99.5% CI for the mean surgery time is (131.37, 142.43).

c) We can calculate the level of confidence, calculating the z-score for the margin of error in that interval.

We know that the difference between the upper bound and lower bound is 2 times the margin of error:

`UL-LL=2E\\\\E=(UL-LL)/(2)=(139.9-133.9)/(2)=(6)/(2)=3`

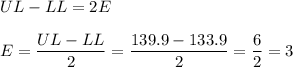
Then, we can write the equation for the margin of error to know the z-value.

`E=z \cdot s/√(n)\\\\z= E\cdot √(n)/s=2*√(132)/22.6=2*11.5/22.6=1.018`

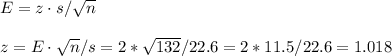
The confidence level for this interval is then equal to the probability that the absolute value of z is bigger than 1.018:

`P(-|z|<Z<|z|)=P(-1.018<Z<1.018)=0.69`

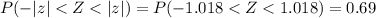
The level of confidence of the interval (133.9, 139.9) is 69%.

d) We have to calculate the sample size n to have a margin of error, for a 95% CI, that is equal to 3.

The critical value for a 95% CI is z=1.96.

Then, the sample size can be calculated as:

`E=z\cdot s/√(n)\\\\n=((z\cdot s)/(E))^2=((1.96*22.6)/(3))^2=14.77^2=218.015\approx 219`

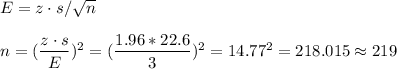
The sample size should be 219 surgeries.

e) We have to calculate the sample size n to have a margin of error, for a 99% CI, that is equal to 3.

The critical value for a 99% CI is z=2.576.

Then, the sample size can be calculated as:

`E=z\cdot s/√(n)\\\\n=((z\cdot s)/(E))^2=((1.96*22.6)/(3))^2=19.41^2=376.59\approx 377`

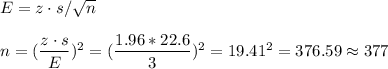
The sample size should be 377 surgeries.