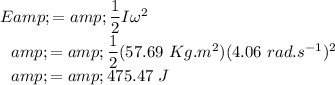Question

A horizontal 826 N merry-go-round of radius 1.17 m is started from rest by a constant horizontal force of 57.8 N applied tangentially to the merry-go-round. Find the kinetic energy of the merry-goround after 3.47 s. The acceleration of gravity is 9.8 m/s 2 . Assume the merry-go-round is a solid cylinder. Answer in units of J. 028 10.0

Answer 1

The kinetic energy of the merry-go-round is
`\bf{475.47~J}`.

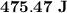Step-by-step explanation:

Given:

Weight of the merry-go-round,
`W_(g) = 826~N`

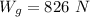
Radius of the merry-go-round,
`r = 1.17~m`

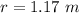
the force on the merry-go-round,
`F = 57.8~N`

Acceleration due to gravity,
`g= 9.8~m.s^(-2)`

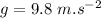
Time given,
`t=3.47~s`

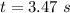
Mass of the merry-go-round is given by

`m &=& (W_(g))/(g)\\~~~~&=& (826~N)/(9.8~m.s^(-2))\\~~~~&=& 84.29~Kg`

Moment of inertial of the merry-go-round is given by

`I &=& (1)/(2)mr^(2)\\~~~&=& (1)/(2)(84.29~Kg)(1.17~m)^(2)\\~~~&=& 57.69~Kg.m^(2)`

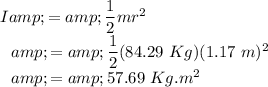
Torque on the merry-go-round is given by

`\tau &=& F.r\\~~~&=& (57.8~N)(1.17~m)\\~~~&=& 67.63~N.m`

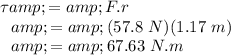
The angular acceleration is given by

`\alpha &=& (\tau)/(I)\\~~~&=& (67.63~N.m)/(57.69~Kg.m^(2))\\~~~&=& 1.17~rad.s^(-2)`

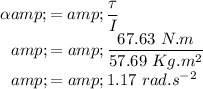
The angular velocity is given by

`\omega &=& \alpha.t\\~~~&=& (1.17~rad.s^(-2))(3.47~s)\\~~~&=& 4.06~rad.s^(-1)`

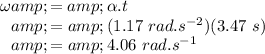
The kinetic energy of the merry-go-round is given by

`E &=& (1)/(2)I\omega^(2)\\~~~&=&(1)/(2)(57.69~Kg.m^(2))(4.06~rad.s^(-1))^(2)\\~~~&=& 475.47~J`