Question

A publisher reports that 47%47% of their readers own a personal computer. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 280280 found that 43%43% of the readers owned a personal computer. Make the decision to reject or fail to reject the null hypothesis at the 0.010.01 level.

Answer 1

The null hypothesis was not rejected.

The proportion of readers who own a personal computer is 47%.

Explanation:

The claim made by a publisher is that 47% of their readers own a personal computer.

A single proportion z-test can be used to determine whether the claim made by the publisher is authentic or not.

The hypothesis for this test can be defined as follows:

H₀: The proportion of readers who own a personal computer is 47%, i.e. p = 0.47.

Hₐ: The proportion of readers who own a personal computer is different from 47%, i.e. p ≠ 0.47.

The information provided is:

`n=280\\\hat p=0.43\\\alpha =0.01`

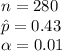
The test statistic is:

`z=\frac{\hat p-p}{\sqrt{(p(1-p))/(n)}}=\frac{0.43-0.47}{\sqrt{(0.47(1-0.47))/(280)}}=-1.34`

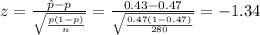
The test statistic value is, z = -1.34.

Decision rule:

If the p-value of the test is less than the significance level α = 0.01 then the null hypothesis will be rejected and vice-versa.

Compute the p-value as follows:

`p-value=2* P (Z < z)`

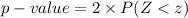
`=2* P (Z < -1.34)\\=2* [1-P(Z<1.34)]\\=2* [1-0.90988]\\=0.18024\\\approx0.18`

*Use a z table for the probability.

The p-value of the test is 0.18.

p-value = 0.18 > α = 0.01

The null hypothesis was failed to be rejected at 1% level of significance.

Conclusion:

There is enough evidence to support the claim made by the publisher. Hence, it can be concluded that the proportion of readers who own a personal computer is 47%.