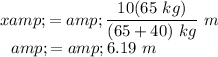Answer:
The distance traveled by the skater is
 .
.
Step-by-step explanation:
Given:
The mass of the first skater is,
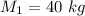 .
.
The mass of the second skater is,
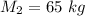
The distance between the skaters is,
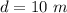
As the skaters are moving towards each other, their center of mass will always be at rest.
Consider that the center of mass is at point C, as shown in the figure. Let's assume that the distance of center of mass from Skater A is
 .
.
From the figure, we can write
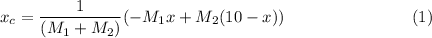
where
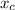 is the position of center of mass along the pole.
is the position of center of mass along the pole.
As the center of mass is at rest, substituting
 for
for
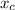 in equation (1), we have
in equation (1), we have
![&& 0 = (1)/((M_(1) + M_(2)))[-M_(1)x + (10 - x)M_(2)]\\&or,& x = (10M_(2))/((M_(2) + M_(1)))~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)](https://img.qammunity.org/2021/formulas/physics/high-school/ax9seluhds9uh1j7pfvc9q06aqz70ortrr.png)
Substituting
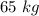 for
for
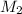 and
and
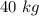 for
for
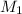 in equation (2), we have
in equation (2), we have