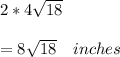Question

A company designed and sells an ultrasonic​ receiver, which detects sounds unable to be heard by the human ear. The receiver can detect mechanical and electrical sounds such as leaking​ gases, air,​ corona, and motor friction noises. It can also be used to hear​ bats, insects, and even beading water. The receiver is 1818 in. deep. The focus is 6 in.6 in. from the vertex. Find the diameter of the outside edge of the receiver.

Answer 1

the diameter of the outside edge of the receiver is
`8√(18) \ \ \ inches`

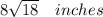
Step-by-step explanation:

From the schematic free body diagram illustrating what the question is all about below;

Let represent A to be the vertex where the receiver is being placed

S to be the focus

BP to be equal to r (i.e radius of the outer edge)

BC to be 2 r (i.e the diameter)

Given that AS = 4 in and AP is 18 in

Let AP be x- axis and AY be y -axis

A=(0,0)

S=(4,0) = (0,0)

So that the equation of the parabolic path of the receiver will be:

`y^2 =4 ax \\ \\ y^2 = 4*4*x \\ \\ y^2 = 16x`

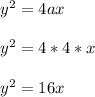
B = (AP, BP)

B = (18, r)

B lies y² = 16 x

r² = 16 x

r² 16 × 18

`r = √(16*18 ) \\ \\ r = 4√(18)`

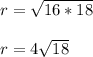
Diameter BC = 2r

`2* 4√(18) \\ \\= 8√(18 ) \ \ \ inches`