Answer:
X is a solution of the system.
Explanation:
To verify that the vector X is a solution of the given system:
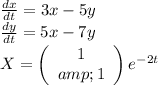
Writing the system in the form X'=AX for some coefficient matrix A, one obtains the following.
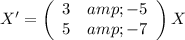
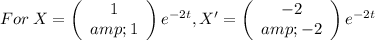
Similarly:

Since the above expressions are equal,
 is a solution of the given system.
is a solution of the given system.