Question

A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 411 gram setting. It is believed that the machine is underfilling the bags. A 26 bag sample had a mean of 406 grams with a variance of 225. Assume the population is normally distributed. A level of significance of 0.02 will be used. Find the P-value of the test statistic. You may write the P-value as a range using interval notation, or as a decimal value rounded to four decimal places.

Answer 1

0.0445937

Explanation:

-Given that the sample statistic has a mean of 406 grams, standard deviation of sq root(225) and the null statistic is 411 grams.

-Assuming normal distribution, the test statistic is calculated as:

`z=(Sample \ statistic-Null \ statistic)/(\sigma/√(n))\\\\=(406-411)/(√(225/26))\\\\=-1.6997`

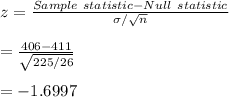
-we then find the p-value of the test statistic from the z-tables:

P-value=0.0445937