Answer:
∴73,563 calls are made between two cities with populations of 100,000 and 160,000 that are 435 miles apart.
Explanation:
Given that,
The number of phone calls between two cities (N )
- directly proportional as the value of populations
 and
and
 of two cities.
of two cities. - Inversely varies as the magnitude of distance (d).
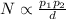
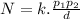
Given that,
N=18,000, d=310 miles,
 =15,500 and
=15,500 and
 =180,000
=180,000
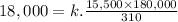
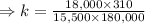

Now,
N=? , d=435 miles,
 =100,500 and
=100,500 and
 =160,000
=160,000
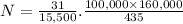
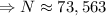
∴73,563 calls are made between two cities with populations of 100,000 and 160,000 that are 435 miles apart.