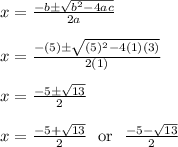Problem 1
We have something in the form
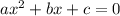 , where
, where
Those values are plugged into the quadratic formula as shown below.
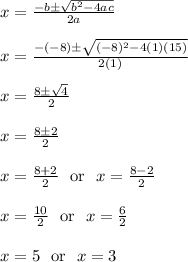
The roots or solutions are x = 5 and x = 3
To check these answers, plug them back into the original equation and you should get the same number on both sides. You can also use a graphing calculator to confirm the answers. In this case, the parabola crosses the x axis at 5 and 3.
======================================================
Problem 2
This time we have
which leads to:
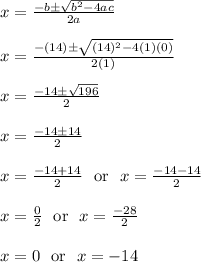
======================================================
Problem 3
We'll plug in a = 1, b = -5, and c = 1
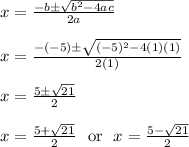
Unlike the previous results, we cannot simplify the square roots down to some whole number. So we leave the roots as they are.
======================================================
Problem 4
We first need to move the 12 over to the left side so that we have 0 on the right side.
The equation
 becomes
becomes
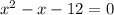 at which point we have
at which point we have
So,

======================================================
Problem 5
Start by subtracting 5 from each side
The equation
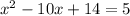 becomes
becomes
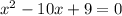
We'll plug in a = 1, b = -10, c = 9
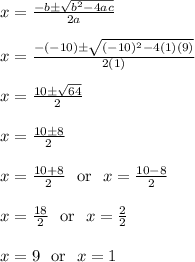
======================================================
Problem 6
This is similar to the first three problems where the equation is already in
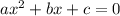 form.
form.
This time we have a = 1, b = 5, c = 3.