Answer:
(a) The sample mean startup cost is 107.3 thousand dollars.
The sample mean startup cost is 107.3 thousand dollars.
(b) The 90% confidence interval for the population average startup costs for candy store franchises is ($89.4, $125.2) thousand.
Explanation:
The questions asked related to the data are:
(a) Use a calculator with mean and sample standard deviation keys to find the sample mean startup cost x and sample standard deviation s. (Round your answers to one decimal place.)
x = thousand dollars
s = thousand dollars
(b) Find a 90% confidence interval for the population average startup costs μ for candy store franchises. (Round your answers to one decimal place.)
lower limit thousand dollars
upper limit thousand dollars
Solution:
The data provided is:
X = {100, 170, 133, 93, 75, 94, 116, 100, 85}
(a)
Compute the sample mean as follows:

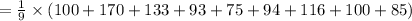
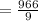
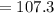
The sample mean startup cost is 107.3 thousand dollars.
Compute the sample standard deviation as follows:
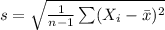
![=\sqrt{(1)/(9-1)* [(100-107.33)^(2)+(170-107.33)^(2)+...+(85-107.33)^(2)]}](https://img.qammunity.org/2021/formulas/mathematics/college/9m8cs6h4j198g57ox4p2iakakcqvo1npdk.png)
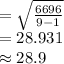
The sample standard deviation of startup cost is 28.9 thousand dollars.
(b)
As the population standard deviation is not known we will use a t-interval.
The critical value of t for 90% confidence level and (n - 1) = 8 degrees of freedom is:

*Use a t-table for the value.
Compute the 90% confidence interval for population mean as follows:
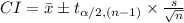

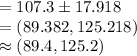
Thus, the 90% confidence interval for the population average startup costs for candy store franchises is ($89.4, $125.2) thousand.