Answer:
If you center the series at x=1
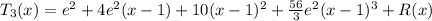
Where
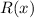 is the error.
is the error.
Explanation:
From the information given we know that

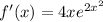 (This comes from the chain rule )
(This comes from the chain rule )
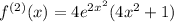 (This comes from the chain rule and the product rule)
(This comes from the chain rule and the product rule)
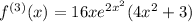 (This comes from the chain rule and the product rule)
(This comes from the chain rule and the product rule)
If you center the series at x=1 then
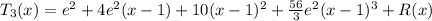
Where
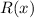 is the error.
is the error.