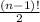Answer:
Explanation:
Let us consider n beads of different colors, arranged in a line. If the beads were to be arranged in a straight line, there are n! ways to do this.
Now, if the beads were to be in a circular arrangement, a pattern will repeat n times.
So the number of different circular arrangements can be obtained by dividing by n, such that we get
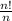 =
=

The patterns can be obtained via rotating either clockwise or anticlockwise, therefore 2 ways. So we can divide the total by 2.
Hence, the different number of necklaces which we can make from n beads of different colors is