Answer:
The critical value for a 98% CI is z=2.33.
The 98% confidence interval for the mean is (187.76, 194.84).
Step-by-step explanation:
We have to develop a 98% confidence interval for the mean number of minutes per day that children between the age of 6 and 18 spend watching television per day.
We know the standard deveiation of the population (σ=21.5 min.).
The sample mean is 191.3 minutes, with a sample size n=200.
The z-value for a 98% CI is z=2.33, from the table of the standard normal distribution.
The margin of error is:
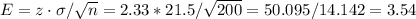
With this margin of error, we can calculate the lower and upper bounds of the CI:
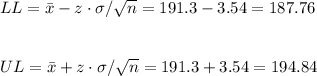
The 98% confidence interval for the mean is (187.76, 194.84).