Answer: The optimal order quantity would be 95 approximately.
Step-by-step explanation:
Since we have given that
Mean = 100 cartons
SD= 20 cartons
Cost price per carton = $50.00
Selling price per carton = $70.00
Salvage cost = $20.00
Underage cost = Selling price - cost price
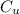 =
=
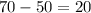
Overall cost = Cost price - Salvage
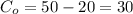
So optimality proportion would be
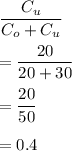
At p = 0.4, so z = -0.253
So, it becomes,

So, the optimal order quantity would be 95 approximately.