Question

Daily demand for fresh cauliflower in the ZZ-Warehouse store follows normal distribution with mean 100 cartons and s.d. 20 cartons. The ZZ-Warehouse buys at a cost of $50.00 per carton, sells it for $70.00 per carton. Unsold cartons are sold for $20.00 per carton. What is the optimal order quantity, using the single period model?

Answer 1

Answer: The optimal order quantity would be 95 approximately.

Step-by-step explanation:

Since we have given that

Mean = 100 cartons

SD= 20 cartons

Cost price per carton = $50.00

Selling price per carton = $70.00

Salvage cost = $20.00

Underage cost = Selling price - cost price

`C_u` =
`70-50=20`

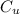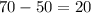
Overall cost = Cost price - Salvage

`C_o=50-20=30`

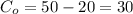
So optimality proportion would be

`(C_u)/(C_o+C_u)\\\\=(20)/(20+30)\\\\=(20)/(50)\\\\=0.4`

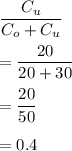
At p = 0.4, so z = -0.253

So, it becomes,

`q=\mu+z* \sigma\\\\q=100-0.253* 20\\\\q=100-5.06\\\\q=94.94`

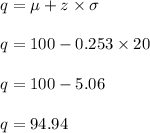
So, the optimal order quantity would be 95 approximately.