Answer:
90 televisions and 89 video cassette recorders
Explanation:
The unit cost of television = $360
The unit cost of video cassette recorder = $270
Let "T" represent the number of televisions and "R" represent the number of recorders, so that we can make representations using equations from the statements.
At the beginning of the week, Total Stock is worth $56,430, where
Total Stock = Total cost of televisions + Total cost of recorders
Total Cost = Unit Cost × Number of items
$56,430 = 360T + 270R This is the first equation
Next, During the week, Number of Sales =
 T +
T +
 R
R
Total Sales Price = 360 (
 T) + 270 (
T) + 270 (
 R)
R)
$32,310 = 270T + 90R This is the second equation
Solving both equations simultaneously, let us use elimination method which involves equating one of the two terms in both equations. Let us multiply the second equation by 3. This doesn't affect the equation, since we are doing it to all the terms in it.
56,430 = 360T + 270R
32,310 = 270T + 90R × 3
So, we have;
56,430 = 360T + 270R
96,930 = 810T + 270R
Subtracting both equations, we have;
96,930 - 56,430 = 810T - 360T
40,500 = 450T
T =
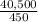 = 90
= 90
Since we now have the number of televisions, we can get the number of recorders by putting 90 in any (say, the second) equation.
32,310 = 270 (90) + 90R
32,310 = 24,300 + 90R
32,310 - 24,300 = 90R
8010 = 90R
R =
 = 89
= 89
At the beginning of the week, the store had 90 televisions and 89 video cassette recorders